Wie weit kann man einen Meteor sehen?
>Ich bekomme E-Mails.
Die meisten stellen Fragen verschiedener Art, von denen die meisten ziemlich einfach zu beantworten sind (tatsächlich könnte vieles durch googeln, Hinweis-Tipp beantwortet werden). Aber manchmal bekomme ich eine Frage, die schwieriger zu beantworten ist, oder sogar eine, über die ich mich selbst gewundert habe, aber nie dazu gekommen bin, sie herauszufinden.
Ich war also ziemlich fasziniert, als ich eine Frage von Bad Reader Dean Lewis über Meteore bekam. Während des Perseiden-Meteorschauers 2018 war er von seiner Familie weg, rund 1.000 Kilometer getrennt. Wenn er einen Meteor sah, war es dann möglich, dass sie denselben von ihrem weiter entfernten Standort aus sehen konnten?
Die kurze Antwort lautet: Ja! Die lange Antwort ist … Mathe. Coole, lustige Mathematik.
Und da, wenn dieser Artikel veröffentlicht wird, der jährliche Geminiden-Meteorschauer 2018 heute Abend seinen Höhepunkt erreicht, denke ich, dass es angemessen ist, dies herauszufinden.
Crashkurs Astronomie: Meteore, Meteoroiden und Meteoriten, oh mein!
Wenn die Erde vollkommen flach wäre, könnte man im Prinzip einen Meteor bis an jeden Rand der Erde sehen. Solange Sie sich über dem Boden befinden, auch nur ein kleines bisschen, dann erreicht Ihre Sichtlinie jeden Quadratzentimeter des Planeten auf Ihrer Seite, sodass jeder Meteor für jeden sichtbar ist. In Wirklichkeit ist die Luft nicht ganz durchsichtig, so dass man aus einiger Entfernung durch so viel Dreck guckt, dass man nichts sehen kann.
Die Erde ist jedoch nicht flach. Ernsthaft! Es ist rund. Und die Atmosphäre umgibt es wie eine Muschel, wird mit der Höhe dünner und verblasst schließlich; diese Höhe hängt von Ihrer Definition von Raum ab. Allerdings können wir ein bisschen schummeln, denn wir kennen die Wissenschaft: Meteore wie in Schauern neigen dazu, etwa 100 Kilometer über dem Boden zu verglühen. Diese Höhe hängt von vielen Dingen ab, einschließlich der Größe der Meteoroiden (die festen Teile interplanetarer Trümmer, die durch den Weltraum rasen) sind, wie schnell sie sich bewegen, in welchem Winkel sie in die Atmosphäre eintreten und so weiter. Aber nennen wir es 100 km.
Shaun der toten Elternführer
Ein Meteor kann Ihnen am nächsten sein, wenn Sie sich direkt darunter befinden und dann 100 km geradeaus (in Ihrem Zenit) sind. Wenn es weiter weg vom Zenit verbrennt, dann muss es weiter von dir entfernt sein. Es liegt nahe, dass man einen Meteor am weitesten entfernt sehen kann, wenn er sich genau am Horizont befindet.
Die Geometrie sieht so aus (Hinweis: NICHT maßstabsgetreu):
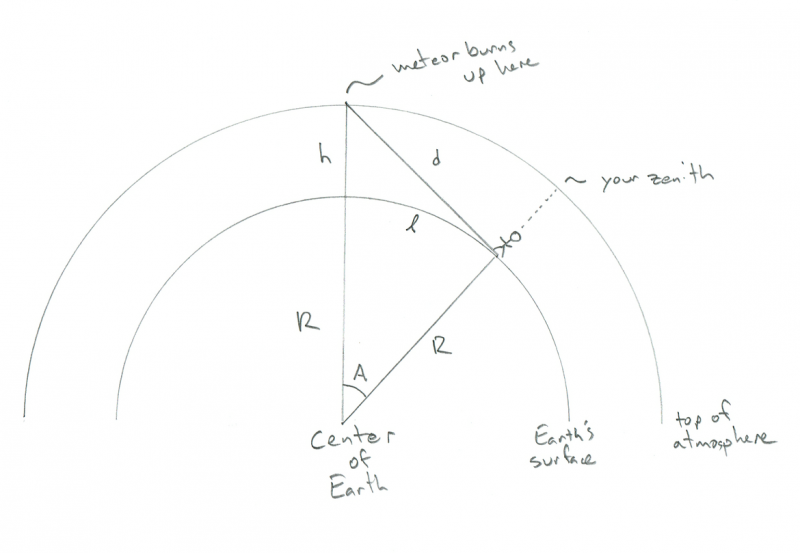
Schema, das die Geometrie eines Beobachters zeigt, der einen Meteor beim Verbrennen beobachtet. Bildnachweis: Phil Plait
Sie können den kleinen Strichmännchen-Menschen auf der Oberfläche der gekrümmten Erde sehen – sagen wir, das sind Sie – mit der (ebenfalls gekrümmten) Atmosphäre darüber. In diesem Diagramm ist R der Radius der Erde (6.4000 km), h ist die Höhe, die der Meteor verbrennt (100 km) und d ist die Entfernung von Ihnen zum Meteor. A ist der Winkel zwischen Ihrer Position auf der Erde und der Position des Meteors darüber, und kursiv l (wie in der Länge) ist die Entfernung, die Sie gehen müssen, damit der Meteor direkt über Ihnen ist (ich weiß, das scheint eine seltsame Sache zu sein) wissen wollen, aber ertragen Sie mit mir). Seltsamerweise kannst du hier alles berechnen, was du brauchst, ohne d zu kennen, aber komm schon, es ist cool zu wissen, wie weit der Meteor entfernt ist, oder?
Der Schlüssel zu all dem ist zu sehen, dass der Winkel zwischen dem Meteor, Ihnen und dem Erdmittelpunkt ein rechter Winkel ist. Das liegt daran, dass sich der Meteor aus Ihrer Sicht am Horizont befindet (oder, wenn Sie einen lustigen Jargon bevorzugen, auf der Tangente des inneren Kreises, wo R ihn schneidet). Das macht das Dreieck zu einem rechtwinkligen Dreieck, und wenn Sie sich an Ihre High-School-Mathematik erinnern, bedeutet das, dass Sie alle Seiten und Winkel finden können!
Merken der Satz des Pythagoras ? In einem rechtwinkligen Dreieck ist das Quadrat der Länge der Hypotenuse gleich der Summe der Quadrate der anderen beiden Seiten*. In unserem Dreieck ist die Hypotenuse R+h und die anderen Seiten sind R und d.
So
(R+h)2= d2+ R2
Tagebuch eines großartigen freundlichen Kindes: Rowley Jeffersons Tagebuch
oder die linke Seite ausmultiplizieren (verwenden Sie VEREITELN ):
R2+ 2Rh + h2 = d2+ R2
Löse nach d auf, um zu sehen, wie weit der Meteor von dir entfernt ist. Beachten Sie, dass R2 auf beiden Seiten ist, also brechen Sie sie ab, um zu erhalten
D2= 2Rh + h2
Oder
d = Quadratwurzel (2Rh + h2)
Nun, wir kennen all diese Zahlen! Plug-n-tuck, Baby:
d = Quadratwurzel (2 x 6.400 x 100 + 10.000) = 1.136 km
Aha! Das bedeutet, dass ein Meteor am Horizont über 1.100 Kilometer entfernt ist! Das ist ein langer Weg und technisch gesehen am weitesten entfernt, um einen Meteor vom Boden aus zu sehen.
Jetzt suchen wir kursiv l. Zuerst müssen wir den Winkel A kennen. Das erfordert etwas Trigonometrie. Da sind viele trig identitäten Sie können das herausfinden, aber mein Favorit†ist, dass in einem rechtwinkligen Dreieck der Sinus eines Winkels die Länge der gegenüberliegenden Seite geteilt durch die Länge der Hypotenuse ist. Wenn wir dieses Verhältnis erhalten, können wir den umgekehrten Sinus (oder Arkussinus) verwenden, um den Winkel zu erhalten.
Spickzettel Engelszahlen
sin (A) = d / (R + h)
so
A = ohne-1(d / R + h)
Plug-n-tuck wieder, und ich bekomme A = 10°. Das ist ein anständiger Teil der Erdoberfläche!
Und jetzt können wir kursives l bekommen. Es gibt 360° um die Erde und der Umfang der Erde beträgt 2 x pi x Radius = 40.192 km, also gibt es
40.192 km / 360° = 112 Kilometer pro Grad
was wiederum 10° = 1.120 Kilometer bedeutet. Das ist ziemlich nahe an d, was nicht allzu überraschend ist. Die Zeichnungen sind übertrieben, aber in Wirklichkeit ist die Lufthülle über uns klein im Vergleich zur Größe der Erde. Wenn ich die Zeichnungen maßstabsgetreu angefertigt hätte, würden Sie sehen, dass d und l wirklich ziemlich ähnlich lang sind.
Okay, also warum bin ich so heiß und mache mir die Mühe, mich zu finden? Wegen der ursprünglichen Frage! Wenn Sie nach all der Mathematik vergessen haben, wie weit können zwei Menschen entfernt sein und immer noch denselben Meteor sehen?
Nun, in diesem Fall wäre der Meteor direkt zwischen ihnen und an jedem ihrer jeweiligen Horizonte. Diese Geometrie sieht so aus:
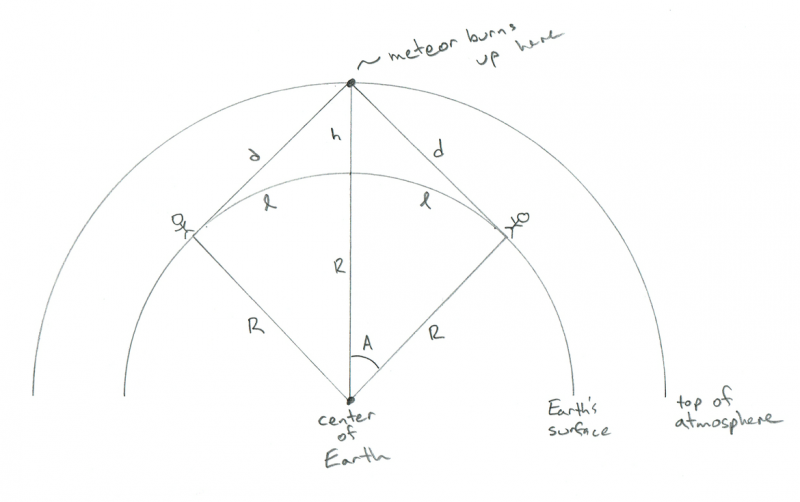
Schema, das die Geometrie zweier Beobachter zeigt, die genau zwischen sich einen Meteoriten verbrennen. Bildnachweis: Phil Plait
AHA! Jetzt siehst du, warum ich mich will! Der Abstand zwischen den beiden Personen beträgt gerade mal 2 x l! Jetzt haben wir also die Antwort:
Damit zwei Menschen denselben Meteor sehen, dürfen sie nicht mehr als 2 x 1.120 = 2.240 Kilometer voneinander entfernt sein. Das ist zum Beispiel ziemlich nah an der Entfernung zwischen Washington, DC und Denver. Beeindruckend.
Übrigens, für einen Perspektivwechsel (wörtlich) bedeutet dies aus der Sicht des Meteors, dass er eine 2.240 Kilometer breite Erdausdehnung sehen kann (wie in DC am östlichen Rand der Erde und Denver am westlichen). Das ist ziemlich toll.
für welches alter ist eine falte in der zeit angemessen
Und das bringt uns zur eigentlichen Antwort auf Deans Frage: Wenn er 1.000 km von seiner Familie entfernt wäre, dann ja, technisch gesehen könnten sie denselben Meteor sehen. Wie ist es damit?
Dies setzt nun wieder voraus, dass die Luft vollkommen klar ist und all das, was in Wirklichkeit im Wesentlichen unmöglich ist. Diese Mathematik stellt also eine ideale Situation dar (einschließlich der Idee, dass sich der Meteor genau zwischen ihnen befindet).
Seien wir realistischer. Nehmen wir an, der Meteor verglüht für beide Beobachter in einer Höhe von 45° über dem Horizont am Himmel. Wie weit würden sie voneinander entfernt sein? Nun, wieder angenommen, der Meteor befindet sich genau zwischen ihnen, ist die Geometrie eher wie folgt:
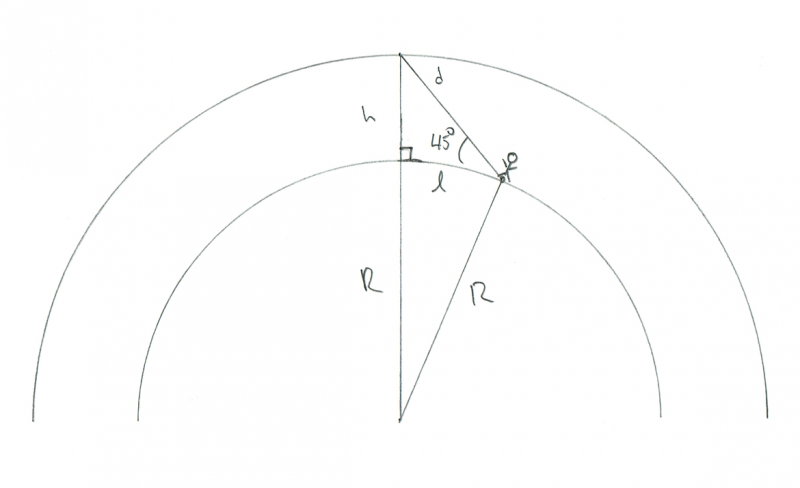
Schematische Darstellung der Geometrie eines Beobachters, der einen Meteor beobachtet, der 45° über dem Horizont aufbrennt. Bildnachweis: Phil Plait
Das ist tatsächlich schwieriger zu lösen, aber ich kenne einen anderen Trick: Wenn wir annehmen, dass l klein ist, dann spielt die Erdkrümmung keine Rolle. Wenn ich zum Beispiel den Abstand zwischen zwei Bäumen in meinem Garten wissen möchte, ist es mir egal, dass die Erde gekrümmt ist. Über eine so kleine Distanz kann ich davon ausgehen, dass es flach ist. Lassen Sie uns diese Annahme hier treffen.
In diesem Fall haben wir ein weiteres rechtwinkliges Dreieck, aber diesmal ist der rechte Winkel der unter dem Meteor. Ich habe es sogar im Diagramm mit der kleinen quadratischen Notation beschriftet. Wenn das also ein 90°-Winkel ist und unser Winkel zum Meteor 45° beträgt, dann beträgt der letzte Winkel (vom Meteor zum Beobachter) ebenfalls 45°. Das bedeutet, dass dies ein gleichschenkliges Dreieck sein muss, also sind l und h gleich! Da wir wissen, dass h 100 km beträgt, muss auch l sein.
Und das bedeutet, dass die Entfernung zwischen unseren beiden Beobachtern doppelt so groß ist, also 200 km.
Die Entfernung zum Meteor beträgt in diesem Fall übrigens etwa 141 km. Die Bestätigung überlasse ich dem Leser als Übung.
Im Prinzip bedeutet dies, dass Sie, wenn Sie wissen, wie hoch ein Meteor vom Horizont entfernt ist und in welcher Höhe er verglüht, seine Entfernung berechnen können (oder wenn Sie die Entfernung kennen, können Sie seine Höhe ermitteln). Dieser Trig ist jedoch ziemlich kompliziert, und ich denke, ich habe dir für heute genug Mathematik auf den Kopf geworfen.
Aber es ist cool zu denken, dass ein bisschen High-School-Mathe eine so lustige Anwendung haben kann. Und ich gebe zu, es ist poetisch und romantisch zu wissen, dass es möglich ist, einen Shooting-Star mit jemand anderem zu teilen, solange die Trennung nicht zu weit ist. Was für ein schöner Gedanke.
* In Der Zauberer von Oz , die Vogelscheuche hat das falsch verstanden nach er hat ein Gehirn.
† Von Kurs Ich habe eine Lieblingstriggeridentität. Welches ist deins?